A Fancier Algorithm

Last week I wrote:

But PloddingPlayer is useful. Within the next two weeks I’ll write fancier algorithms that require much more CPU time and memory. If they can’t beat this algorithm, I’ll know I have a problem.

And that is exactly what happened.

Minimax

Suppose you’re playing Phutball as Left, and the board looks like this:

Notation: Some people say that “one turn ahead” means (a) “I make a move and then my opponent moves”, whereas some people say it means (b) “I make a move”. To resolve this confusion, game theorists talk in terms of “plies”, where (a) is two plies and (b) is one ply.

If you’re thinking one ply ahead, you’d move the ball to the east like so:

But if you’re thinking two plies ahead, you’d realize your opponent would then jump the ball back towards your goal:

If you’re thinking three plies ahead, you might put a man three squares to the right of the ball:

No matter how your opponent replies, you can then jump three squares to the right on your next turn (i.e. 3 plies in the future).

But if you’re thinking four plies ahead, you’d realize that your opponent could place a man just above the one you placed:

Then you jump:

And then they respond (on the 4th ply in the future) by jumping northwest, west, north, and west:

This sort of thinking—“If I do this, my opponent will do that, and then I’ll respond with this…”—can be formalized as the minimax algorithm.1 I implemented this algorithm for Phutball.

Testing minimax

The practical limit for how far my computer can look ahead in Phutball is 4 plies.

It takes about 15 seconds for the algorithm to search 3 plies in the future, but it takes about 16 minutes to look 4 plies ahead. Why? The number of positions increases exponentially. On average, there are 50 million positions you could be in after 4 plies2. Although I haven’t tried it, I’d guess it’d take about 17 hours to search 5 plies ahead.

Searching 50 million positions sounds very impressive, until I discovered that minimax could not defeat PloddingPlayer.3 Highlights of their game:

After 32 plies, it looked good for minimax (playing as Right), which had forced the ball 4 columns to the left:

But after 64 plies, there wasn’t any progress:

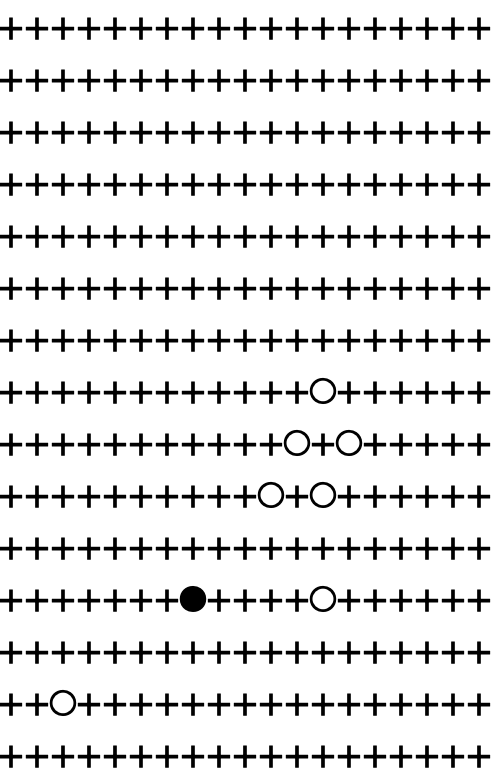
Nor after 96 plies:

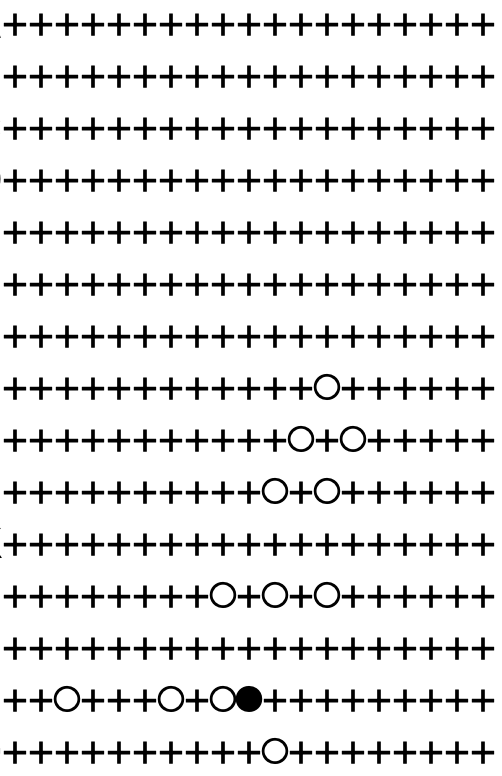
After 18 hours, I called a halt at move 133:

This is a little vexing. PloddingPlayer is so simplistic that it takes about 0.01 seconds to choose a move. On average, minimax requires 980 seconds to move, and yet they’re evenly matched. If you only allow the minimax algorithm to search 3 plies ahead, it loses to PloddingPlayer in 47 moves.

But there are ways to improve minimax, and I ought to be able to cook something up in a week or two.

Footnotes:

1

Technically, I’m using negamax, but they’re essentially the same thing.

2

[mathjax] These are just the end nodes of the game tree. Note that I’ve pruned this number down quite a bit. The computer only checks positions where you put a man within 2 squares of another piece. Otherwise, I estimate that there’d be about \( (19 \cdot 15)^4 = 6.6 \cdot 10^9 \) positions after 4 plies.

3

The full list of moves in this game is here.