Groundhog Day
EDIT: 2021-04-11: The next post will appear on May 5. (You may notice that this is after the CATAM is due.)
tl;dr: Once again I make a sophisticated algorithm; once again PloddingPlayer beats it. This is a little embarrassing.
In theory
I suspected that Minimax (the program I wrote last time) couldn’t beat PloddingPlayer because it wasn’t very good at deciding how promising a position was. For instance, consider these 3 positions:



The first one is Phutball’s initial position; the second is a win for Right; the third is a win for Left. But Minimax only ranked positions based on the left-right coordinate of the ball. The worst score is 0 (the ball is in your goal); the best score is 1 (the ball is in your opponent’s goal). If Minimax saw these boards as possible outcomes 4 plies (i.e. 4 moves) in the future, it would rank them as 0.5, equally good.
Of course, if Minimax had the processing power to look 5 plies ahead, it would see that these boards lead to wildly different outcomes. But I don’t have that processing power.
Ideally we’d want a function that takes the current board as input and quickly outputs the score that Minimax would have given the board if Minimax had spent time examining all the future possibilities.
For instance, suppose we had this board as input:
The output should be 0, indicating that Right will get the ball in Left’s goal soon.
But I don’t know how to write such a function.
And if you don’t know how to do something, you get a neural network to do it for you.
That is, we ask Minimax to look into the future of this position and give us the score. Then we do that for about 20000 other positions. So we have 20000 ordered pairs of the form (input board, output score).
(My laptop ran for about 98 hours to get this data.)
And then we train a neural network on that data, i.e. the neural network learns the correct parameters to become the function we need. It’s magic.
OK, it’s not really magic:
But you don’t need to know how a neural network works in order to do cool stuff like teach a computer to recognize pictures of sandals and sneakers.
The neural network shouldn’t be trained on all 20000 data points.1 If it just memorized the correct output for every input, it would be useless. We need it to generalize—to give scores to boards it hasn’t been trained on.
So I didn’t let the neural network see 20% of the data (which isn’t exactly 4000 data points; it’s 4667). Then I tested the network’s accuracy (difference between Minimax’s score and the neural network’s predicted score) on those 4667 inputs.
The average difference2 was 0.0637, which is pretty good, considering a score can be anywhere between 0 and 1. For instance, when I apply the neural network to the above board, it predicts that Minimax will score it as 0.0008, which is really close to 0.
We make a new version of Minimax (call it Minimax 2.0, and call the original 1.0) that uses this improved function to judge how promising a board position is.
In practice
PloddingPlayer wiped the floor with Minimax 2.0. Here’s a game where PloddingPlayer was Right, trying to shift the ball to the left.
After 5 moves:

After 10 moves:

After 15 moves:

And PloddingPlayer has jumped the ball off the board into Left’s goal after the 20th move:

If we randomize the initial moves, PloddingPlayer still wins easily.
I think the problem is that my 20000 data points came from games that Minimax 1.0 played against itself. Although almost all of these games were different (I randomized the first 6 moves of each game), I’m guessing that there were some patterns.
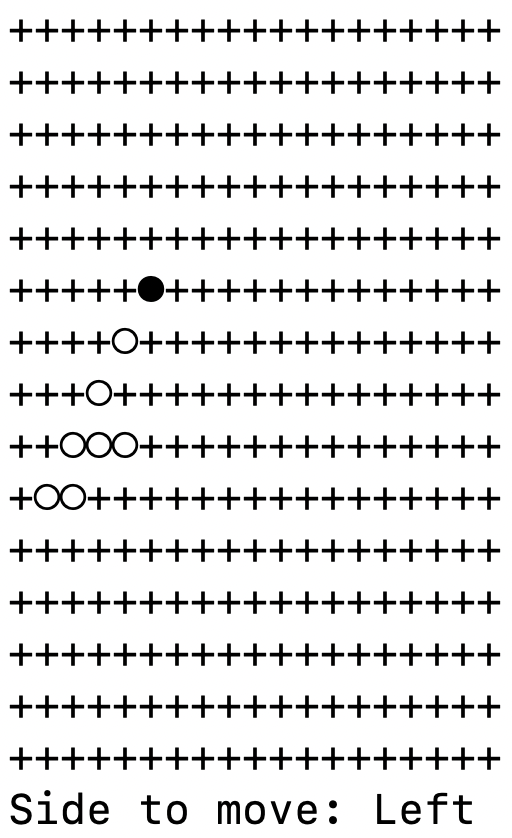
For instance, Minimax 2.0 (playing as Left) thinks it’s about to win this position, even though in fact Right wins on its next move:

Maybe Left really did win every position like this in the training data, since the ball was always in a convenient position for Left? I don’t know for sure.
Until (if) I can make a better algorithm, PloddingPlayer is the undisputed champion.
Footnotes:
Actually, I had just over 23000 data points. My training set had 19000 data points, and my test set had 4667 data points.
mean of the absolute values of the differences


